Forecasting with Markov switching models
Forecasts from Markov switching models have, by and large, disappointed. In a recent paper with Tom Boot, we investigated this issue.
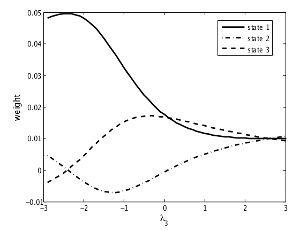
Our starting point is the observation that, conditional on the states, standard Markov switching forecasts do not use all data. This cannot be optimal. Instead, our approach uses all data and weights them such that our forecast loss function is optimised. In this paper, we use the mean square forecast error (MSFE) and derive weights such that the MSFE is minimised.
This work is based on previous results for break point models, where the weights are based on the DGP and estimates of parameters are plugged in to make them operational. In that case, using a plug-in version of the weights lead to forecasts that have an MSFE similar to standard forecasts. Markov switching models allow us to address this point.
The results are quite informative.
-
Incorporating uncertainty around the states in the derivation of the optimal weights, improves forecasts dramatically – and this is even true asymptotically.
-
The common finding that Markov switching models have nice in-sample properties but do poorly out-of-sample is largely based on the selection of the forecast evaluation period. In the paper, we show that, in a symmetric three state Markow switching model, the linear model (i.e. without Markov switching) will be the optimal model for forecasting in the middle regime. In empirical forecast evaluations of Markov switching models, the typical forecasting period has been dominated by the great moderation. This is precisely the middle regime where the optimal forecast from the Markov switching model is the same as the forecast from the linear model.
The paper is on my research page or download the latest pdf file directly.